Question

The ΔH for the solution process when solid sodium hydroxide dissolves in water is 44.4 kJ/mol. When a 6.21-g sample of NaOH dissolves in 250.0 g of water in a coffee-cup calorimeter, the temperature increases from 23.0 °C to ________°C. Assume that the solution has the same specific heat as liquid water, i.e., 4.18 J/g-K.

Answer 1

Answer: The final temperature of the solution is 29.6°C

Step-by-step explanation:

To calculate the number of moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

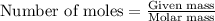
Given mass of NaOH = 6.21 g

Molar mass of NaOH = 40 g/mol

Putting values in above equation, we get:

`\text{Moles of NaOH}=(6.21g)/(40g/mol)=0.155mol`

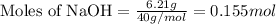
To calculate the enthalpy change of the reaction, we use the equation:

`\Delta H_(rxn)=(q)/(n)`

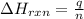
where,

q = amount of heat absorbed = ?

n = number of moles = 0.155 moles

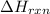`\Delta H_(rxn)` = enthalpy change of the reaction = 44.4 kJ/mol = 44400 J/mol (Conversion factor: 1 kJ = 1000 J)

Putting values in above equation, we get:

`44400J/mo=(q)/(0.155mol)\\\\q=(44400J/mol* 0.155mol)=6882J`

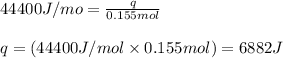
To calculate the heat absorbed by the calorimeter, we use the equation:

`q=mc\Delta T`

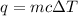
where,

q = heat absorbed = 6882 J

m = mass of water = 250 g

c = heat capacity of solution = 4.18 J/g.K = 4.18 J/g°C

`\Delta T` = change in temperature =
`T_2-T_1=(T_2-23)^oC`

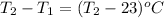
Putting values in above equation, we get:

`6882J=250g* 4.18J/g^oC* (T_2-23)\\\\T_2=29.6^oC`

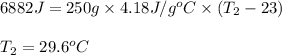
Hence, the final temperature of the solution is 29.6°C