Question

The weight of corn chips dispensed into a bag by the dispensing machine has been identified as possessing a normal distribution with a mean of 14.5 ounces and a standard deviation of 0.2 ounces. Suppose 100 bags of chips are randomly selected. Calculate the z-score if the mean weight of the 100 bags is 14.6 ounces.

A. .6915
B. .1915
C. .3085
D. approximately 0

Answer 1

D. The z- score of the bags is equal to a value of 0.

Explanation:

The probability that a normally distributed data with statndard deviation σ and a mean, μ,exceeds a value x, is given by

P(X > x)=1-p(X < x)= 1- P(z<
`\frac {x- μ} \frac{{σ}{sqrt η}}`

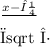
Now,

Given:

weight of corn chips dispensed into a 14-ounce bag by the dispensing machine is a normal distribution with

mean = 14.5 ounces

standard deviation =0.2 ounce.

So,

If 100 bags of chips are randomly selected the probability that the mean weight of these 100 bags exceeds 14.6 ounces is given by:

⇒ P(X> 14.6)= 1- P(z<
`\frac {14.6-14.5} \frac{{0.2}{sqrt 100}}`

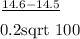
⇒ 1- P(z< 5)=

⇒ 1 - 1 = 0.

Therefore,

The z score of the bags is equal to a value of zero.