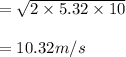Question

If the motor exerts a constant force of 300 N on the cable, determine the speed of the 26-kg crate when it travels s = 10 m up the plane, starting from rest. The coefficient of kinetic friction between the crate and the plane is μk = 0.3.

Answer 1

10.32m/s

Step-by-step explanation:

F = ma

T -mg sinθ-f =ma

We can conclude that T = 300 newtons by taking a freebody of the cable. So we need to determine only the frictional force.

f(n) = 0

mgcosθ = N = 0

N = mgcosθ

T - mg sinθ - u mgcosθ = ma

a = T - mg (sinθ + u cosθ) / m

`a = (300 - 26(9.8)(\sin 30^0 + 0.3 \cos 30^0))/(20)`

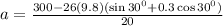
a = 5.32m/s^2

Use constant acceleration kinematics:

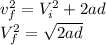
`v_f^2=V_i^2+2ad\\V_f^2 = √(2ad)`

=
`= √(2* 5.32*10) \\\\=10.32m/s`