Question

A block (mass 5 kg ) sits at rest. A second block (mass 10 kg ) collides with the first block, initially moving with a speed of 12 m/s just before the collision. After the collision, the two blocks stick together, and they slide for 4 s across a rough surface before coming to a stop. What was the magnitude of the average force of friction acting on the blocks after the collision?

Answer 1

Answer: The magnitude of the average force of friction acting on the blocks after the collision is 30 N.

Step-by-step explanation:

According to the conservation of momentum,

`m_(1)v_(1) + m_(2)v_(2) = (m_(1) + m_(2))v_(f)`

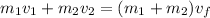
Putting the given values into the above formula as follows.

`m_(1)v_(1) + m_(2)v_(2) = (m_(1) + m_(2))v_(f)`

`0 + 10 * 12 = (5 + 10)v_(f)`

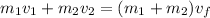
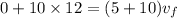
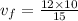`v_(f) = (12 * 10)/(15)` m/s

We assume that acceleration due to friction is
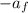`-a_(f)`. Also,

v = u + at

Here, v = 0 m/s

u = 8 m/s

t = 4 sec

Then, value of acceleration will be as follows.

v = u + at

`0 = 8 + a * 4`

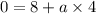
a = 2
`m/s^(2)`

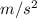
Now, we know that expression for frictional force is as follows.

`F_(f) = (m_(1) + m_(2)) * a_(f)`

=
`15 * 2`

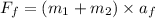
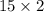
= 30 N

Thus, we can conclude that the magnitude of the average force of friction acting on the blocks after the collision is 30 N.