Question

An insurance company hired your group to help investigate an insurance claim following a car accident. In the accident, two cars collided in an intersection – one (mass 1650kg) was traveling north before the collision, while the other (1900kg) was traveling east. As part of your investigation, you need to determine if either driver was violating the posted speed limit before the collision. Each road had a speed limit of 40 miles per hour (17.9m/s). A traffic camera confirms that the car initially traveling north was going a bit under the speed limit at 16m/s. Furthermore, you know that after the collision, the two cars stuck together and slid a total distance of 13m from the point where they collided. The coefficient of kinetic friction between their tires and the road is 0.7.Was the eastbound car exceeding the posted speed limit before the collision?

Answer 1

as v₂ is greater than v the car exceeds the speed limit before the collision.

Step-by-step explanation:

The conservation of momentum is:

P = P₁ + P₂

P = m₁v₁ + m₂v₂

(1650 + 1900)v = (1650*16)i + (1900v₂)i

3550v = 1900v₂i + 26400i (eq. 1)

The work is:

`-F_(k) d=-(1)/(2) mv^(2) \\-u_(k) mgd=-(1)/(2) mv^(2) \\u_(k) gd=(1)/(2) v^(2) \\v=\sqrt{2u_(k)gd } =√(2*0.7*9.8*13) =13.35m/s`

Replacing in eq. 1

`v=(1900v_(2) )/(3550) i+(26400)/(3550) i\\v=\sqrt{((1900)/(3550))^(2)v_(2)^(2)+((26400)/(3550) )^(2) } \\v_(2) =0.29v_(2)^(2) +55.3\\13.35^(2) =0.29v_(2)^(2) +55.3\\v_(2) =\sqrt{(13.35^(2)-55.3 )/(0.29) } =20.6m/s`

as v₂ is greater than v the car exceeds the speed limit before the collision.

Answer 2

v=8m/s

Step-by-step explanation:

To solve this problem we have to take into account, that the work done by the friction force, after the collision must equal the kinetic energy of both two cars just after the collision. Hence we have

`W_(f)=E_(k)\\W_(f)=\mu N=\mu(m_1+m_1)g\\E_(k)=(1)/(2)[m_1+m_2]v^2`

where

mu: coefficient of kinetic friction

g: gravitational acceleration

We can calculate the speed of the cars after the collision by using

`W_f=(0.7)(1650kg+1900kg)(9.8(m)/(s^2))=24353J\\24353J=(1)/(2)(1650kg+1900kg)v^2\\v=\sqrt{(24353J)/(1775kg)}=3.70(m)/(s)`

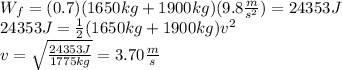
Now , we can compute the speed of the second car by taking into account the conservation of the momentum

`P_b=P_a\\m_1v_1+m_2v_2=(m_1+m_2)v\\\\v_2=((m_1+m_2)v-m_1v_1)/(m_1)\\\\v_2=((1650kg+1900kg)(3.7(m)/(s))-(1650kg)(16(m)/(s)))/((1650kg))\\\\v_2=8(m)/(s)`

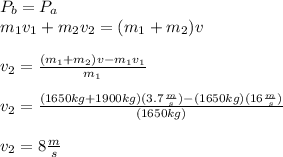
the car did not exceed the speed limit

Hope this helps!!