Answer:
The specific heat of the object
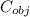 = 0.457
= 0.457
Step-by-step explanation:
Mass of the object
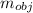 = 23.2 gm
= 23.2 gm
Initial temperature
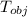 = 97 ° c
= 97 ° c
Mass of the water
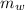 = 90 gm
= 90 gm
Initial temperature of water
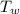 = 20.5 ° c
= 20.5 ° c
Final temperature of both water & object
 = 22.6 ° c
= 22.6 ° c
It is given that heat lost by the object = heat gain by the water
⇒
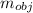
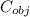 (
(
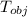 -
-
 ) =
) =
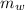
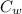 (
(
 -
-
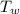 )
)
Put all the values in above formula we get
⇒ 23.2 ×
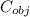 ( 97 - 22.6 ) = 90 × 4.18 × ( 22.6 - 20.5 )
( 97 - 22.6 ) = 90 × 4.18 × ( 22.6 - 20.5 )
⇒
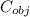 = 0.457
= 0.457
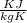
This is the specific heat of the object.