Answer:
T = 1.57 seconds
Step-by-step explanation:
The interpretation of the question is:
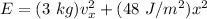
What is the period of the oscillation?
Now; the actual energy of the linear oscillationis:

The first part is used in solving the kinetic energy and the second part is used in solving the potential energy, it is in the potential part that the information about the period is hidden.
So, let go by the potential part by comparing them with our given question:
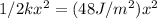
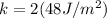
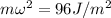
There is need for the mass of the oscillating body, so we take the kinetic part and then compare with our given question:
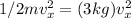
m = 6kg
Substituting m= 6 kg in the equation above; we have:
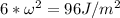
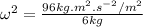
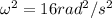
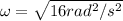
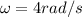
Using;
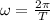 to determine the period
to determine the period
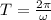
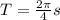
T = 1.57 seconds