Question

Chlorine atoms react with methane, forming HCl and CH3. The rate constant for the reaction was determined to be 3.600×107 at 278 K and 3.050×108 at 317 K. Calculate the activation energy for the reaction. (in kJ mol^-1)

Answer 1

Answer: The activation energy for the reaction is 40.143 kJ/mol

Step-by-step explanation:

To calculate activation energy of the reaction, we use Arrhenius equation for two different temperatures, which is:

`\ln((K_(317K))/(K_(278K)))=(E_a)/(R)[(1)/(T_1)-(1)/(T_2)]`

where,

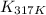`K_(317K)` = equilibrium constant at 317 K =
`3.050* 10^(8)M^(-1)s^(-1)`

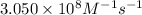
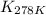`K_(278K)` = equilibrium constant at 278 K =
`3.600* 10^(7)M^(-1)s^(-1)`

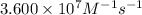
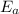`E_a` = Activation energy = ?

R = Gas constant = 8.314 J/mol K

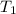`T_1` = initial temperature = 278 K

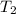`T_2` = final temperature = 317 K

Putting values in above equation, we get:

`\ln((3.050* 10^8)/(3.600* 10^(7)))=(E_a)/(8.314J/mol.K)[(1)/(278)-(1)/(317)]\\\\E_a=40143.3J/mol=40.143kJ/mol`

Hence, the activation energy for the reaction is 40.143 kJ/mol