1 Answer

Willwsharp · Answer 1 · 2021-03-14T02:10:19+0000

Given that the two functions are
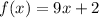f(x)=9x+2 and
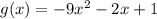
g(x)=-9x^2-2x+1

We need to determine the value of
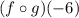
$(f \circ g)(-6)$

The value of
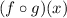$(f \circ g)(x)$ :

The value of
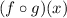$(f \circ g)(x)$ can be determined using the formula,

$(f \circ g)(x)=f[g(x)]$

Substituting
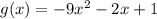g(x)=-9x^2-2x+1 in the above formula, we get;

$(f \circ g)(x)=f[-9x^2-2x+1]$

Now, substituting
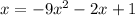x=-9 x^(2)-2 x+1 in the function
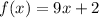f(x)=9x+2 , we get;

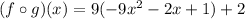
$(f \circ g)(x)=9(-9x^2-2x+1)+2$

$(f \circ g)(x)=-81x^2-18x+9+2$

$(f \circ g)(x)=-81x^2-18x+11$

Thus, the value of
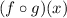$(f \circ g)(x)$ is
$(f \circ g)(x)=-81x^2-18x+11$

The value of
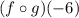$(f \circ g)(-6)$ :

The value of
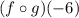$(f \circ g)(-6)$ can be determined by substituting x = -6 in the function
$(f \circ g)(x)=-81x^2-18x+11$

Thus, we have;

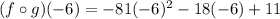
$(f \circ g)(-6)=-81(-6)^2-18(-6)+11$

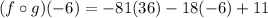
$(f \circ g)(-6)=-81(36)-18(-6)+11$

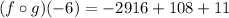
$(f \circ g)(-6)=-2916+108+11$

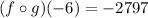
$(f \circ g)(-6)=-2797$

Thus, the value of
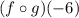$(f \circ g)(-6)$ is -2797

Hence, Option B is the correct answer.

Please log in or register to add a comment.