Answer:
46.57
Explanation:
Given that:
h(t) = 37t - 4.9t²
When the ball reaches the ground, then the height is zero;
So, we equate h(t) to zero and solve for t
37t - 4.9t² = 0
t = 0, 7.55
Let the Initial time be a = t = 0
The time the ball reaches the ground be b = 7.55
So, the average height can now be calculated as:
Average height =

=
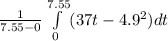
=

=
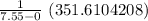
= 46.57091665
≅ 46.57 to (2 decimal places)