Question

A manufacturer makes integrated circuits that each have a resistance layer with a target thickness of 200 units. A circuit won't work well if this thickness varies too much from the target value. These thickness measurements are approximately normally distributed with a mean of _______.

Answer 1

probability P = 0.32

Step-by-step explanation:

this is incomplete question

i found complete A manufactures makes integrated circuits that each have a resistance layer with a target thickness of 200 units. A circuit won't work well if this thickness varies too much from the target value. These thickness measurements are approximately normally distributed with a mean of 200 units and a standard deviation of 12 units. A random sample of 17 measurements is selected for a quality inspection. We can assume that the measurements in the sample are independent. What is the probability that the mean thickness in these 16 measurements x is farther than 3 units away from the target value?

solution

we know that Standard error is expess as

Standard error =
`(sd)/(√(n))`

Standard error =
`(12)/(√(16))`

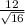
Standard error = 3

so here we get Z value for 3 units away are from mean are

mean = -1 and + 1

so here

probability P will be

probability P = P( z < -1 or z > 1)

probability P = 0.1587 + 0.1587

probability P = 0.3174

probability P = 0.32