Answer:
a) Ф
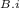 =
=
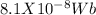 , Ф
, Ф
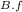 = 0
= 0
b) E = 0.52mV
Step-by-step explanation:
a) considering the loop of wire which has an area of A = 11.6cm² and N = 250 turns, it is initially placed perpendicularly in the earth magnetic field. Then it is rotated from this position to a position where its plane is parallel to the field as shown in the following figure in Δt = 0.040s. Given that the earths magnetic field at the position of the loop is B = 7.0 x
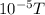 , the flux through the loop before it is rotated is:
, the flux through the loop before it is rotated is:
Ф
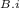 = BAcos(Ф
= BAcos(Ф
 ) = BAcos(0°)
) = BAcos(0°)
Ф
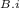 =(7.0 x
=(7.0 x
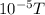 )(11.6 x
)(11.6 x
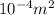 )(1)
)(1)
Ф
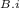 =
=
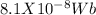
Ф
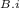 =
=
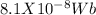
after it is rotated the angle between the area and the magnetic field is Ф = 90°, hence
Ф
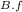 = BAcos(Фf) = BAcos(90°) = 0
= BAcos(Фf) = BAcos(90°) = 0
b) The average magnitude of the emf induced in the coil equals the change in the flux divided by the time of this change, and multiplied by the number of turns that is
|Eav| = N | ФB,f - ФB,i |/ Δt
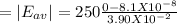
= 5.2 x
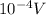
E = 0.52mV