Answer:
(a) 0.0869
(b) 0.0668
(c) 0.8463
Explanation:
We are given that the thickness measurements of ancient prehistoric Native American pot shards discovered in a Hopi village are approximately normally distributed, with a mean of 4.9 millimeters (mm) and a standard deviation of 1.4 mm.
Let X = thickness measurements of ancient prehistoric Native American pot shards
The z-score probability distribution is given by ;
Z =
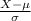 ~ N(0,1)
~ N(0,1)
where,
 = mean thickness = 4.9 mm
= mean thickness = 4.9 mm
 = standard deviation = 1.4 mm
= standard deviation = 1.4 mm
The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.
(a) Probability that the thickness is less than 3.0 mm is given by = P(X < 3.0 mm)
P(X < 3.0 mm) = P(
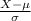 <
<
 ) = P(Z < -1.36) = 1 - P(Z
) = P(Z < -1.36) = 1 - P(Z
 1.36)
1.36)
= 1 - 0.9131 = 0.0869
The above probability is calculated using z table by looking at value of x = 1.36 in the z table which have an area of 0.9131.
(b) Probability that the thickness is more than 7.0 mm is given by = P(X > 7.0 mm)
P(X > 7.0 mm) = P(
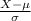 >
>
 ) = P(Z > 1.50) = 1 - P(Z
) = P(Z > 1.50) = 1 - P(Z
 1.50)
1.50)
= 1 - 0.9332 = 0.0668
The above probability is calculated using z table by looking at value of x = 1.50 in the z table which have an area of 0.9332.
(c) Probability that the thickness is between 3.0 mm and 7.0 mm is given by = P(3.0 mm < X < 7.0 mm) = P(X < 7.0 mm) - P(X
 3.0 mm)
3.0 mm)
P(X < 7.0 mm) = P(
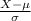 <
<
 ) = P(Z < 1.50) = 0.9332 {using z table}
) = P(Z < 1.50) = 0.9332 {using z table}
P(X
 3.0 mm) = P(
3.0 mm) = P(
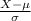

 ) = P(Z
) = P(Z
 -1.36) = 1 - P(Z < 1.36)
-1.36) = 1 - P(Z < 1.36)
= 1 - 0.9131 = 0.0869
Therefore, P(3.0 mm < X < 7.0 mm) = 0.9332 - 0.0869 = 0.8463