Question

SABA claims that about 85 percent of students of East Brunswick High Schools (EBHS) experience difficulty with socializing and getting a sense of belonging. YASI wants to test this claim, so she randomly samples 60 students and finds that 45 have experienced difficulty. Test SABA’s claim at the 95% level of confidence.A. Yes. SABA’s claim is valid.

B. No. SABA’s claim is not valid.
C. Both a and b are correct, depending on the total number of students of EBHS.
D. None of the above.

Answer 1

No, SABA’s claim is not valid.

Explanation:

We are given that SABA claims that about 85 percent of students of East Brunswick High Schools (EBHS) experience difficulty with socializing and getting a sense of belonging. YASI wants to test this claim, so she randomly samples 60 students and finds that 45 have experienced difficulty.

We have to test this claim of SABA.

Firstly, let p = percent of students of East Brunswick High Schools (EBHS) who experience difficulty with socializing and getting a sense of belonging

So, Null Hypothesis,
`H_0` : p = 85% {means that the SABA’s claim is valid}

Alternate Hypothesis,
`H_a` : p
`\\eq` 85% {means that the SABA’s claim is not valid}

The test statistics that will be used here is One-sample z-test statistics,i.e;

T.S. =
`\frac{\hat p-p}{\sqrt{(p(1- p))/(n) } }` ~ N(0,1)

where,
`\hat p` = percent of students of East Brunswick High Schools (EBHS) who experience difficulty with socializing and getting a sense of belonging in a sample of 60 students =
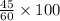`(45)/(60) * 100` = 75%

n = sample of students = 60

So, test statistics =
`\frac{0.75-0.85}{\sqrt{(0.85(1-0.85))/(60) } }`

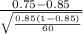
= -2.17

Now, at 5% significance level z table gives critical values of -1.96 and 1.96. Since our test statistics does not lies in between the critical values of z so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that SABA’s claim is not valid.

Answer 2

B. No. SABA’s claim is not valid.

Explanation:

We have to perform a hypothesis test on proportions.

The null and alternative hypothesis are:

`H_0:\pi=0.85\\\\H_a: \pi\\eq0.85`

The level of significance is
`\alpha=0.05`.

The sample proportion is

`p=X/n=45/60=0.75`

The standard deviation is:

`\sigma=\sqrt(\pi(1-\pi))/(n)=\sqrt(0.85\cdot 0.15)/(60)=0.0461`

Then, we can calculate the z-statistic as:

`z=(p-\pi+0.5/n)/(\sigma)=(0.75-0.85+0.00)/(0.0461) =(-0.10)/(0.0461) =-2.17`

The P-value for a two-tails test and z=-2.17 is P=0.03.

The P-value is smaller than the significance level, so the effect is significant.

The null hypothesis is rejected.

The SABA's claim of p=0.85 is not valid.