Question

One yard crew works four times faster than the other yard crew. If they work together they can finish a job in 60 minutes. How fast each yard crew works?

Answer 1

The second yard crew works for 48 minutes.

The first yard crew works for 12 minutes which is four times faster that the second crew.

Explanation:

Let us assume,

The second yard crew completes the work in 'x' minutes.

It is given that,

• The first yard crew works four times faster than the other yard crew.
• Therefore, first yard crew will complete the work in 'x/4' minutes.

If they work together they can finish a job in 60 minutes.

⇒ x + x/4 = 60 minutes.

⇒ 5x / 4 = 60

⇒ x = 240/5

⇒ x = 48 minutes.

Therefore, the second yard crew works for 48 minutes.

To find the first yard crew :

We already know that, they are 4 times faster that the second yard crew.

Substitute x = 48 in x/4,

⇒ 48 ÷ by 4

⇒ 12 minutes.

Therefore, the first yard crew works for 12 minutes which is four times faster that the second crew.

Answer 2

Time taken by both crew is 48 min and 12 min , when they work together !

Explanation:

Here we have , One yard crew works four times faster than the other yard crew. If they work together they can finish a job in 60 minutes. We need to find How fast each yard crew works . Let's find out:

One yard crew works four times faster than the other yard crew

Let speed of one crew be x , So speed of other crew is four times i.e.

⇒
`4x`

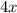
If they work together they can finish a job in 60 minutes.

According to above statement , both can finish work in 60 min i.e.

⇒
`4x+x=60`

⇒
`5x=60`

⇒
`x=12`

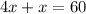
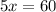
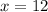
So , time taken by other crew is 4x = 4(12) = 48 min . Therefore , Time taken by both crew is 48 min and 12 min , when they work together !