Question

Samantha pushes a 116 kgkg crate on a ramp that makes 17.2 degreesdegrees with the horizontal. What is the change in potential energy of this crate after Samantha pushes it for 2.50 mm along the ramp? (The answer choices have 3 significant figures.)

Answer 1

The change in potential energy of the crate is 0.840 J.

Step-by-step explanation:

Given:

Mass of the crate (m) = 116 kg

Acceleration due to gravity (g) = 9.8 m/s²

Angle of inclination of ramp (x) = 17.2°

Displacement of the crate along the ramp (d) = 2.50 mm = 0.0025 m

Displacement, being a vector quantity, can be resolved along the horizontal and vertical directions. The vertical component represents the change in height of the crate.

Now, the vertical height of the crate is equal to the vertical component of the displacement and is given as:

`h=d\sin x\\\\h=0.0025* \sin(17.2^\circ)\\\\h=7.39* 10^(-4)\ m`

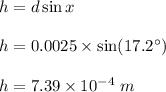
Now, the change in potential energy of the crate is given by the formula:

`\Delta U=mgh`

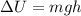
Here, ΔU → Change in gravitational potential energy

Plug in the given values and solve for 'ΔU'. This gives,

`\Delta U=116* 9.8* 7.39* 10^(-4)\ J\\\\\Delta U=0.840\ J`

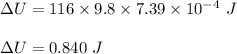
Therefore, the change in potential energy of the crate is 0.840 J.