Question

[Q71 Suppose that the height, in inches, of a 25-year-old man is a normal random variable with parameters g = 71 inch and 02 = 6.25 inch2 (a) What percentage of 25- year-old men are over 6 feet, 2 inches tall? (b) What percentage of 25-year-old men in the 6-footer club are over 6 feet, 5 inches?

Answer 1

Answer: (a) Percentage of 25 year old men that are above 6 feet 2 inches is 11.5%.

(b) Percentage of 25 year old men in the 6 footer club that are above 6 feet 5 inches are 2.4%.

Explanation:

Given that,

Height (in inches) of a 25 year old man is a normal random variable with mean
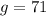`g=71` and variance
`o^(2) =6.25`.

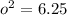To find: (a) What percentage of 25 year old men are 6 feet, 2 inches tall

(b) What percentage of 25 year old men in the 6 footer club are over 6 feet. 5 inches.

Now,

(a) To calculate the percentage of men, we have to calculate the probability

P[Height of a 25 year old man is over 6 feet 2 inches]= P[X>
`74in`]

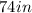P[X>74] = P[
`(X-g)/(o)` >
`(74-71)/(2.5)`]

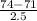= P[Z > 1.2]

= 1 - P[Z ≤ 1.2]

= 1 - Ф (1.2)

= 1 - 0.8849

= 0.1151

Thus, percentage of 25 year old men that are above 6 feet 2 inches is 11.5%.

(b) P[Height of 25 year old man is above 6 feet 5 inches gives that he is above 6 feet] = P[X,
`6ft`
`5in` - X,
`6ft`]

P[X >
`6ft`
`5in` I X >
`6ft`] = P[X > 77 I X > 72]

=
`(P[X > 77])/(P[ X > 72])`

=
`(P[(X - g)/(o)>(77-71)/(2.5)] )/(P[(X-g)/(o) >(72-71)/(2.5)] )`

=
`(P[Z >2.4])/(P[Z>0.4])`

=
`(1-P[Z\leq2.4] )/(1-P[Z\leq0.4] )`

=
`(1-0.9918)/(1-0.6554)`

=
`(0.0082)/(0.3446)`

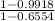
= 0.024

Thus, Percentage of 25 year old men in the 6 footer club that are above 6 feet 5 inches are 2.4%.