Question

Use Lagrange multipliers to find the volume of the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the given plane. x + 9y + 4z = 27

Answer 1

The volume of the largest rectangular box (V) = 81/4

Explanation:

Step 1:-

Given volume of the largest rectangular box in the first octant

V = l b h

let (x ,y, z) be the one vertex in the given plane

V = f(x, y, z) = x y z

given plane. Ф (x, y, z) = x + 9y + 4z = 27 ........(1)

Step( ii):

By using Lagrange multipliers

Suppose it is required to find the extreme for the function f(x, y, z) subject to the condition Ф (x, y, z) =0

Form Lagrange function F(x, y, z) = f(x, y, z) + λ Ф (x, y, z) where λ is called the Lagrange multipliers

F(x, y, z) = x y z+ λ ( x + 9y + 4z - 27) ......(2)

Obtain the equations are δ F / δ x = 0

δ f / δ x +λ δ Ф / δ x =0

⇒ y z + λ ( 1) = 0

⇒ y z = - λ ......(a)

Obtain the equations are δ F / δ y = 0

δ f / δ x +λ δ Ф / δ x =0

⇒ x z + λ ( 9) = 0

⇒
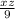`(xz)/(9)` = - λ .......(b)

Obtain the equations are δ F / δ z = 0

δ f / δ x +λ δ Ф / δ z =0

x y + λ ( 4) = 0

⇒
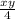`(xy)/(4)` = - λ .......(c)

Step (iii):-

Equating (a) and (b) equations

we get
`y z = (xz)/(9)`

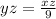
cancel 'z' value we get x = 9y .......(d)

Equating (b) and (c) equations

we get
`(xy)/(4) = (xz)/(9)`

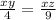
cancel 'x' value on both sides , we get

4z =9y ......(e)

substitute (d) (e) values in equation (1) we get

x + 9y + 4z -27 = 0

9y + 9y + 9y -27 =0

27y -27 =0

y = 1

substitute y =1 in x = 9y

x = 9

substitute y =1 in 4z =9y

z = 9 /4

therefore the dimensions are x =9 , y=1 and z = 9 /4

Conclusion:-

The largest volume of the rectangular box V = x y z

substitute x =9 , y=1 and z = 9 /4

V = 9(1)(9/4) =81/4

The largest volume of the rectangular box (V) = 81/4

Verification :-

Given plane x + 9y + 4z = 27

substitute x =9 , y=1 and z = 9 /4

9 + 9 + 4(9/4) = 27

27 =27

so satisfied equation