Question

A battery manufacturer advertises that the mean reserve capacity of a certain battery is 1500 hours. You suspect that the batteries’ reserve time is less than the advertised value. To test this claim, you randomly select a sample of 20 batteries and find the mean reserve capacity to be 1320 hours. Assume that the population standard deviation is 320 hours. Do you have enough evidence to support the manufacturer’s claim? What assumption is necessary for this test to be valid? None. The Central Limit Theorem makes any assumptions unnecessary. The population of all the batteries’ reserve time is normally distributed because of the small sample size. The population variance must equal the population mean.

Answer 1

The test statistic t = 2.45 > 1.729

we rejected null hypothesis so the population mean is not equal population variance

Explanation:

The mean reserve capacity of a certain battery is(μ) 1500 hours

Given sample of n = 20 batteries

The sample mean reserve capacity to be (
`x`)=1320 hours.

Assume that the population standard deviation is(σ) = 320 hours

Null hypothesis:H0 = μ = 1500 hours

Alternative hypothesis:H1 = μ ≠ 1500 hours

The test statistic

`t = (x-u)/((σ)/(√(n) ) )`

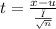
now simplification, we get

`t = (1320-1500)/((320)/(√(20-1) ) )`

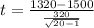
t = modulus(-2.45) = 2.45

Degrees of freedom γ = n-1 = 20-1 =19

By tabulated value in t- distribution at 5% level of significance

tabulated value = 1.729 ( from table)

The calculated value > tabulated value

we rejected null hypothesis .

we rejected null hypothesis so the population mean is not equal population variance