Question

Use the special multiplication rule to find the indicated probability. Find the probability of correctly answering the first 5 questions on a multiple choice test if random guesses are made and each question has 4 possible answers.

Answer 1

0.1% probability of correctly answering the first 5 questions

Explanation:

For each question, there are four possible answers, one of which is correct.

So the probability of getting a question correct is 1/4 = 0.25.

The questions are also independent, that is, the probability of guessing correctly one question does not interfer with other questions. So we can use the special multiplication rule, that is, the probability of events A and B both happening is:

`P(A \cap B) = P(A)*P(B)`

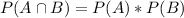
In this problem, there are 5 events(getting each question right) with 0.25 probability. So

`(0.25)^(5) = 0.001`

0.1% probability of correctly answering the first 5 questions