Question

Records of 40 used passenger cars and 40 used pickup trucks (none used commercially) were randomly selected to investigate whether there was any difference in the mean time in years that they were kept by the original owner before being sold. For cars, the mean was 5.3 years with standard deviation 2.2 years. For pickup trucks, the mean was 7.1 years with standard deviation 3.0 years.

Answer 1

There is a difference in the mean time in years that the vehicles were kept by the original owner before being sold.

Explanation:

In this problem we need to test whether the two population mean time (in years) the vehicles were kept by the original owner are equal or not.

Use a two sample z-test to perform the analysis.

The hypotheses is defined as follows:

H₀: The two population means are equal, i.e. µ₁ - µ₂ = 0

Hₐ: The two population means are not equal, i.e. µ₁ - µ₂ ≠ 0.

The provided information:

`n_(1)=n_(2)=40\\\bar x_(1)=5.3\\\bar x_(2)=7.1\\s_(1)=2.2\\s_(2)=3.0`

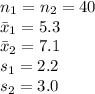
Compute the z-statistic as follows:

`z=\frac{\bar x_(1)-\bar x_(2)}{\sqrt{(s_(1)^(2))/(n_(1))+(s_(2)^(2))/(n_(2))}} =\frac{5.3-7.1}{\sqrt{(2.2^(2))/(40)+(3.0^(2))/(40)}}=-3.06`

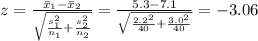
The test statistic value is -3.06.

Compute the p-value of the test as follows:

`p-value=2* P(Z<-3.06)\\=2* [1-P(Z<3.06)]=\\2* (1-0.9989)\\=0.0022`

The p-value of the test is 0.0022.

Decision rule:

If the p-value is less than the significance level of the test then the null hypothesis will be rejected and vice-versa.

The p-value obtained is 0.0022.

This value is very small. So it will be rejected at any significance level.

So, the null hypothesis will be rejected.

Conclusion:

As the null hypothesis is rejected it can be concluded that there is a difference in the mean time in years that the vehicles were kept by the original owner before being sold.