Question

PLEASE HELP!!!!

The following picture is a square pyramid where DE=8 cm and m∠ADE=60°.
Find the surface area of the pyramid in both exact form and approximate form.
Round your approximate answer to one decimal place.
(Make sure you include formulas and numbers in the formulas as part of your solution.
Also include units in your final answers.)

Answer 1

The surface area of the pyramid in exact form is 64 +
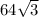`64√(3)` cm²

The approximated surface area of the pyramid is 174.9 cm²

Explanation:

The surface area of the square pyramid is the sum of the area of the base and the area of the four triangular faces

In Δ EFD

∵ m∠EFD = 90°

∵ m∠FDE = 60°

∵ ED = 8 cm

- By using sine ratio to find FE

∵ sin(∠FDE) =
`(FE)/(ED)`

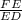
∴ sin(60) =
`(FE)/(8)`

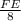
- Multiply both sides by 8

∴ FE = 8 sin(60°)

∴ FE =
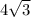`4√(3)` cm

In Δ AED

∵ AE = ED

∵ m∠D = 60°

- In any isosceles Δ if measure of an angle is 60, then the

triangle is equilateral Δ

∴ Δ AED is an equilateral Δ

∴ AD = 8 cm

∵ The pyramid has 4 identical triangular faces

∵ Area of each Δ =
`(1)/(2)` × base × height

∵ AD is the base and FE is the height

∴ Area of each Δ =
`(1)/(2)` × 8 ×
`4√(3)`

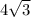
∴ Area of each Δ =
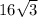`16√(3)` cm²

∵ Surface area of the pyramid = Area of base + 4 area of a Δ

∵ Area of base = 8²

∴ Area of base = 64 cm²

∴ Surface area of the pyramid = 64 + 4 ×
`16√(3)`

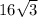
∴ Surface area of the pyramid = 64 +
`64√(3)`

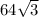
The surface area of the pyramid in exact form is 64 +
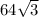`64√(3)` cm²

The approximated surface area of the pyramid is 174.9 cm²