Question

) Suppose that an urn contains 7 green, 8 red, and 9 yellow balls. You pick a ball at random and replace it. You then do this 9 more times (making 10 times altogether). What is the probability that you selected green 2 times, red 3 times, and yellow 5 times?

Answer 1

Probability = 0.0589

Explanation:

The total number of balls in an urn is: 7 + 8 + 9 = 24 balls

The possible arrangements are:
`(10!)/(2!3!5!) = 2520`

Probability of getting a green ball =
`(7)/(24)`.

Probability of getting a red ball =
`(8)/(24)`.

Probability of getting a yellow ball = .

Therefore, the required probability is:

`2520 * ((7)/(24))^2 * ((8)/(24))^3 * ((9)/(24))^5\\ = 2520 * 0.08507 * 0.03704 * 0.00742 \\= 0.0589`

Answer 2

Title:

The required probability is
`2.336* 10^(-5) = 0.00002`.

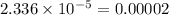Explanation:

In the urn, there are total (7 + 8 + 9) = 24 balls.

We are taking 10 balls out of the urn with replacement.

In each tern, we have overall 10 choices to chose 1 ball.

If we want to get a green, there are 7 choices each time.

Similarly, 8 choices each time for getting a red and 9 choices each time for getting a yellow ball.

The probability of getting green 2 times, red 3 times, and yellow 5 times is
`(7^2 *8^3*9^5)/((24)^(10)) = 2.336 * 10^(-5)`.