Answer:
The distance is the absolute value of the difference.
Explanation:
Given table:
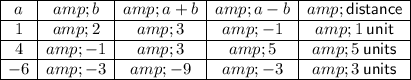
The difference is column 4.
The distance is column 5.
The absolute value of a number is its positive numerical value. It is denoted by a vertical line either side of the real number.
For example, |5| means 'the absolute value of 5', and |-5| means 'the absolute value of -5'.
Taking the absolute values of the differences:
⇒ |-1| = 1
⇒ |5| = 5
⇒ |-3| = 3
Therefore, the distance is the absolute value of the difference.