Answer:
The two diameters that separate the top 5% and the bottom 5% are 5.84 and 5.60 respectively.
Explanation:
We are given that the diameters of bolts produced in a machine shop are normally distributed with a mean of 5.72 millimeters and a standard deviation of 0.07 millimeters.
Let X = diameters of bolts produced in a machine shop
So, X ~ N(
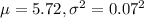 )
)
The z score probability distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = mean diameter = 5.72 millimeter
= mean diameter = 5.72 millimeter
 = standard deviation = 0.07 millimeter
= standard deviation = 0.07 millimeter
Now, we have to find the two diameters that separate the top 5% and the bottom 5%.
- Firstly, Probability that the diameter separate the top 5% is given by;
P(X > x) = 0.05
P(
 >
>
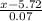 ) = 0.05
) = 0.05
P(Z >
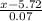 ) = 0.05
) = 0.05
So, the critical value of x in z table which separate the top 5% is given as 1.6449, which means;
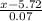 = 1.6449
= 1.6449
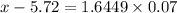
 = 5.72 + 0.115143 = 5.84
= 5.72 + 0.115143 = 5.84
- Secondly, Probability that the diameter separate the bottom 5% is given by;
P(X < x) = 0.05
P(
 <
<
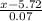 ) = 0.05
) = 0.05
P(Z <
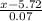 ) = 0.05
) = 0.05
So, the critical value of x in z table which separate the bottom 5% is given as -1.6449, which means;
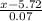 = -1.6449
= -1.6449

 = 5.72 - 0.115143 = 5.60
= 5.72 - 0.115143 = 5.60
Therefore, the two diameters that separate the top 5% and the bottom 5% are 5.84 and 5.60 respectively.