Question

The number of defective parts produced by a process in one day has a Poisson distribution with a mean of 10. Each defective part has probability of 0.6 of being repaired. What is the probability that exactly 12 parts are produced in one day

Answer 1

9.48% probability that exactly 12 parts are produced in one day

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

The number of defective parts produced by a process in one day has a Poisson distribution with a mean of 10.

This means that
`\mu = 10`

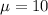
What is the probability that exactly 12 parts are produced in one day

This is P(X = 12).

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 12) = (e^(-10)*(10)^(12))/((12)!) = 0.0948`

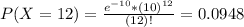
9.48% probability that exactly 12 parts are produced in one day