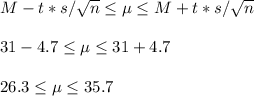Question

A random sample of 15 employees was selected. The average age in the sample was 31 years with a variance of 49 years. Assuming ages are normally distributed, the 98% confidence interval for the population average age is _____.

Answer 1

Assuming ages are normally distributed, the 98% confidence interval for the population average age is [26.3, 35.7].

Explanation:

We have to construct a 98% confidence interval for the mean.

The information we have is:

- Sample mean: 31

- Variance: 49

- Sample size: 15

- The age is normally distributed.

We know that the degrees of freedom are

`k=n-1=15-1=14`

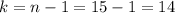
Then, the t-value for a 98% CI is t=2.625 (according to the t-table).

The standard deviation can be estimated from the variance as:

`s=\sqrt {s^2}=√(49)=7`

The margin of error is:

`E=t_(14)*s/√(n)\\\\E=2.625*7/√(15)=18.375/3.873=4.7`

Then, the CI can be constructed as:

`M-t*s/√(n)\leq\mu\leq M+t*s/√(n)\\\\31-4.7\leq \mu \leq 31+4.7\\\\26.3\leq \mu \leq 35.7`