Question

The amount of time that people spend at Grover Hot Springs is normally distributed with a mean of 73 minutes and a standard deviation of 16 minutes. Suppose one person at the hot springs is randomly chosen. Let X = the amount of time that person spent at Grover Hot Springs . Round all answers to 4 decimal places where possible.

Answer 1

(a)
`X\sim N(\mu = 73, \sigma = 16)`

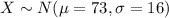
(b) 0.7910

(c) 0.0401

(d) 0.6464

Explanation:

Let X = amount of time that people spend at Grover Hot Springs.

The random variable X is normally distributed with a mean of 73 minutes and a standard deviation of 16 minutes.

(a)

The distribution of the random variable X is:

`X\sim N(\mu = 73, \sigma = 16)`

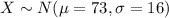
(b)

Compute the probability that a randomly selected person at the hot springs stays longer than 60 minutes as follows:

`P(X>60)=P((X-\mu)/(\sigma)>(60-73)/(16))\\=P(Z>-0.8125)\\=P(Z<0.8125)\\=0.7910`

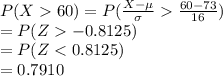
*Use a z-table for the probability.

Thus, the probability that a randomly selected person at the hot springs stays longer than an hour is 0.7910.

(c)

Compute the probability that a randomly selected person at the hot springs stays less than 45 minutes as follows:

`P(X<45)=P((X-\mu)/(\sigma)<(45-73)/(16))\\=P(Z<-1.75)\\=1-P(Z<-1.75)\\=1-0.9599\\=0.0401`

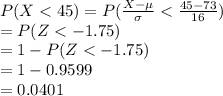
*Use a z-table for the probability.

Thus, the probability that a randomly selected person at the hot springs stays less than 45 minutes is 0.0401.

(d)

Compute the probability that a randomly person spends between 60 and 90 minutes at the hot springs as follows:

`P(60<X<90)=P(X<90)-P(X<60)\\=P((X-\mu)/(\sigma)<(90-73)/(16))-P((X-\mu)/(\sigma)<(60-73)/(16))\\=P(Z<1.0625)-P(Z<-0.8125)\\=0.8554-0.2090\\=0.6464`

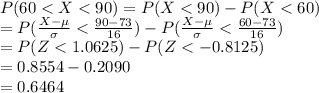
*Use a z-table for the probability.

Thus, the probability that a randomly person spends between 60 and 90 minutes at the hot springs is 0.6464