Question

You are designing a rectangular poster to contain 7575 in2 of printing with a 33​-in margin at the top and bottom and a 11​-in margin at each side. What overall dimensions will minimize the amount of paper​ used?

Answer 1

The dimensions of the rectangular poster is 15 in by 5 in.

Explanation:

Given that, the area of the rectangular poster is 75 in².

Let the length of the rectangular poster be x and the width of the rectangular poster be y.

The area of the poster = xy in².

`\therefore xy=75`

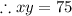
`\Rightarrow y=(75)/(x)`....(1)

1 in margin at each sides and 3 in margin at top and bottom.

Then the length of printing space is= (x-2.3) in

=(x-6) in

The width of printing space is = (y-2.1) in

=(y-2) in

The area of the printing space is A =(x-6)(y-2) in²

∴ A =(x-6)(y-2)

Putting the value of y

`\Rightarrow A =(x-6)((75)/(x)-2)`

`\Rightarrow A = 87-(450)/(x)-2x`

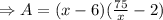
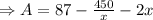
Differentiating with respect to x

`A '= (450)/(x^2)-2`

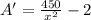
Again differentiating with respect to x

`A''=-(900)/(x^3)`

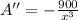
To find the minimum area of printing space, we set A' = 0

`\therefore (450)/(x^2)-2=0`

`\Rightarrow 450 =2x^2`

`\Rightarrow x^2=225`

`\Rightarrow x=\pm 15`

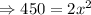
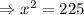
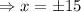
Now putting x=±15 in A''

`A''|_(x=15)=-(900)/(15^3)<0`

`A''|_(x=-15)=-(900)/((-15)^3)=(900)/((15)^3)>0`

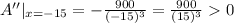
Since at x=15 , A"<0 Therefore at x=15 , the area will be minimize.

From (1) we get

`y=(75)/(x)`

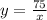
Putting the value of x

`y=(75)/(15)`

=5 in

The dimensions of the rectangular poster is 15 in by 5 in.