Question

A tree growing on a hillside makes a 75° angle with the hill. From a point 80 feet up the hill, the angle of elevation to the top of the tree is 65° and the angle of depression to the bottom is 24°. Find the height of the tree.

Answer 1

height of tree = 290.19 feet

Explanation:

given data

angle with the hill a = 75°

up the hill = 80 feet

elevation to top of tree = 65°

angle of depression to bottom = 24°

solution

we know that Sum of Property of Triangles is

sum of the internal angles of a triangle = 180° ............1

and

Sine Rule is

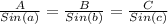`(A)/(Sin(a)) = (B)/(Sin(b)) = (C)/(Sin(c))` .......................2

so here

angle with the hill a = 75°

and

sum of the angle of elevation and angle of depression is

b = 65°+ 24°

b = 89°

and we know

a + b + c = 180°

so c will be

c = 180° - 89° - 75°

c = 16°

so here we get height of the pine tree by equation 2 we get

`(80)/(Sin(16)) = (B)/(Sin(89))`

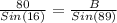
solve it we get

height of tree = 290.19 feet