Question

The time needed to complete a final examination in a particular college course is normally distributed with a mean of 80 minutes and a standard deviation of 10 minutes. Answer the following questions. (a) What is the probability of completing the exam in one hour or less?

Answer 1

0.02275

Explanation:

We have been given that the time needed to complete a final examination in a particular college course is normally distributed with a mean of 80 minutes and a standard deviation of 10 minutes. We are asked to find the probability of completing the exam in one hour or less.

We know that 1 hour equals 60 minutes. First of all, we will find the z-score corresponding to 60 minutes.

`z=(x-\mu)/(\sigma)`

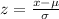
z = z-score,

x = Sample score,

`\mu` = Mean,

`\sigma` = Standard deviation.

`z=(60-80)/(10)`

`z=(-20)/(10)`

`z=-2`

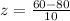
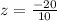
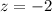
Now, we will use normal distribution table to find area under z-score of
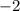`-2` as:

`P(z< -2)`

`P(z< -2)=0.02275`

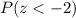
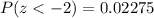
Therefore, the probability of completing the exam in one hour or less is 0.02275.