Question

7.30 A quality-control inspector rejects any shipment of printed circuit boards whenever 3 or more defectives are found in a sample of 50 boards tested. Find the (1) expected number defective and (2) the probability of rejecting the shipment when the proportion of defectives in the entire shipment is

Answer 1

1)
`E(X) = 50*0.01= 0.5`

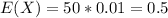
2) The probability of rejecting the shipment is given by:

`P(X \geq 3)`

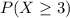
And if we use the complement rule we got:

`P(X \geq 3)=1-P(X<3) = 1-P(X\leq 2) =1-[P(X=0)+P(X=1)+P(X=2)]`

We can find the individual probabilities like this:

`P(X=0)=(50C0)(0.01)^0 (1-0.01)^(50-0)=0.605`

`P(X=1)=(50C1)(0.01)^1 (1-0.01)^(50-1)=0.306`

`P(X=2)=(50C2)(0.01)^2 (1-0.01)^(50-2)=0.076`

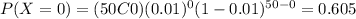
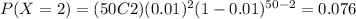
And replacing we got:

`P(X \geq 3)=1-P(X<3) = 1-P(X\leq 2) =1-[0.605+0.306+0.076]=0.013`

Explanation:

Assuming that the proportion of defectives is p=0.01

Previous concepts

A Bernoulli trial is "a random experiment with exactly two possible outcomes, "success" and "failure", in which the probability of success is the same every time the experiment is conducted". And this experiment is a particular case of the binomial experiment.

The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".

The probability mass function for the Binomial distribution is given as:

`P(X)=(nCx)(p)^x (1-p)^(n-x)`

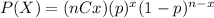
Where (nCx) means combinatory and it's given by this formula:

`nCx=(n!)/((n-x)! x!)`

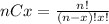
The complement rule is a theorem that provides a connection between the probability of an event and the probability of the complement of the event. Lat A the event of interest and A' the complement. The rule is defined by:
`P(A)+P(A') =1`

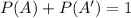
Solution to the problem

Let X the random variable of interest, on this case we now that:

`X \sim Binom(n=50, p=0.01)`

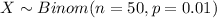
Part 1

For this case the expected number of defectives are:

`E(X) = 50*0.01= 0.5`

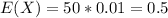
Part 2

The probability of rejecting the shipment is given by:

`P(X \geq 3)`

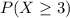
And if we use the complement rule we got:

`P(X \geq 3)=1-P(X<3) = 1-P(X\leq 2) =1-[P(X=0)+P(X=1)+P(X=2)]`

We can find the individual probabilities like this:

`P(X=0)=(50C0)(0.01)^0 (1-0.01)^(50-0)=0.605`

`P(X=1)=(50C1)(0.01)^1 (1-0.01)^(50-1)=0.306`

`P(X=2)=(50C2)(0.01)^2 (1-0.01)^(50-2)=0.076`

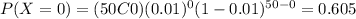
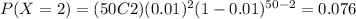
And replacing we got:

`P(X \geq 3)=1-P(X<3) = 1-P(X\leq 2) =1-[0.605+0.306+0.076]=0.013`