Question

A test to determine whether a certain antibody is present is 99.1​% effective. This means that the test will accurately come back negative if the antibody is not present​ (in the test​ subject) 99.1​% of the time. The probability of a test coming back positive when the antibody is not present​ (a false​ positive) is 0.009. Suppose the test is given to four randomly selected people who do not have the antibody. ​(a) What is the probability that the test comes back negative for all four ​people? ​(b) What is the probability that the test comes back positive for at least one of the four ​people? ​(a) Upper P (all 4 tests are negative )equals nothing ​(Round to four decimal places as​ needed.)

Answer 1

( a ) Probability that the test comes back negative for all four ​people = .9723

( b ) Probability that t he test comes back positive for at least one of the four ​people = .0277

Explanation:

Given

The probability of the test will accurately come back negative if the antibody is not present = 99.1
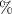`\%` = .991

The probability of the test will accurately come back positive if the antibody is not present = .009

Suppose the test is given to four randomly selected people who do not have the antibody .

( a ) Probability that the test comes back negative for all four ​people =

=
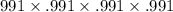`991*.991*.991*.991` = .9723

If we say E = P( all 4 test are negative) or we say E = P( not of the all 4 test are positive)

P( at least one of the 4 test are positive) = 1 - P( not of the all 4 test are positive) = 1 - P( all 4 test are negative)

( b ) Probability that t he test comes back positive for at least one of the four ​people = 1 - P( all 4 test are negative)

= 1 - .9723

= .0277