Answer:
H0 is accepted
there is no difference between the proportions of Indian and Asian young people who listen to rap music every day.
Explanation:
Given a sample survey compared 634 randomly chosen Indians aged 15 to 25 with 567 randomly selected Asians in the same age group.
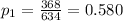
It found that 368 of the Indians and 130 Asians listened to rap music every day.
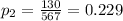
Null hypothesis H0: there is no difference between the proportions of Indian and Asian young people who listen to rap every day.
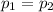
Alternative hypothesis:-
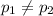
Level of significance α = 0.05
The test of statistic
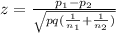
where

p = 0.414
and q = 1-p = 1- 0.414 =0.586
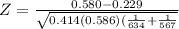
on calculation , we get
z = 0.300 ><1.96 at 95 % level of significance
H0 is accepted
there is no difference between the proportions of Indian and Asian young people who listen to rap every day.