Question

A random sample of 150 men found that 88 of the men excercise regularly, while a random sample 200 women found that 130 of the women exercise regularly. A friend says that she believes that a higher proportion of women then men exercise regularly. Write hypotheses that you could use to test your friend's belief. (Be sure to define the parameters referred to in the hypotheses.) Do not actually perform the test. ONLY write the hypotheses.

Answer 1

Null Hypothesis,
`H_0` :
`p_1 \leq p_2` or
`p_1-p_2 \leq 0`

Alternate Hypothesis,
`H_a` :
`p_1>p_2` or
`p_1-p_2>0`

Explanation:

We are given that a random sample of 150 men found that 88 of the men exercise regularly, while a random sample 200 women found that 130 of the women exercise regularly.

A friend says that she believes that a higher proportion of women then men exercise regularly.

For this firstly;

Let
`p_1` = proportion of women who exercise regularly

`p_2` = proportion of men who exercise regularly

So, Null Hypothesis,
`H_0` :
`p_1 \leq p_2` or
`p_1-p_2 \leq 0`

Alternate Hypothesis,
`H_a` :
`p_1>p_2` or
`p_1-p_2>0`

Here, null hypothesis states that the proportion of women who exercise regularly are less than or equal to the proportion of men who exercise regularly.

Similarly, alternate hypothesis states that proportion of women who exercise regularly are higher than the proportion of men who exercise regularly.

So, this is the correct hypothesis that would be used for conducting the test.

Answer 2

The hypothesis is:

H₀:
`p_(X)-p_(Y)=0`.

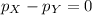Hₐ:
`p_(X)-p_(Y)<0`.

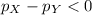Explanation:

Let X = number of men who exercise regularly and Y = number of women who exercise regularly.

The information provided is:

`n_(X)=150\\X=88\\n_(Y)=200\\Y=130`

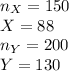
Compute the sample proportion of men and women who exercise regularly as follows:

`\hat p_(X)=(X)/(n_(X))=(88)/(150)=0.587`

`\hat p_(Y)=(Y)/(n_(Y))=(130)/(200)=0.65`

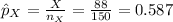
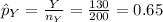
The random variable X follows a Binomial distribution with parameters n = 150 and
`\hat p_(X)=0.587`.

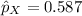The random variable Y also follows a Binomial distribution with parameters n = 200 and
`\hat p_(Y)=0.65`.

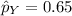According to the Central limit theorem, if from an unknown population large samples of sizes n > 30, are selected and the sample proportion for each sample is computed then the sampling distribution of sample proportion follows a Normal distribution.

The mean of this sampling distribution of sample proportion is:

`\hat p=p`

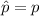
The standard deviation of this sampling distribution of sample proportion is:

`\sigma_(\hat p)=\sqrt{(\hat p(1-\hat p))/(n)}`

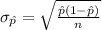
So, the sampling distribution of the proportion of men and women who exercise regularly follows a Normal distribution.

A two proportion z-test cab be performed to determine whether the proportion of women is more than men who exercise regularly.

The hypothesis for this test cab be defined as:

H₀: The proportion of women is same as men who exercise regularly, i.e.
`p_(X)-p_(Y)=0`.

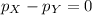Hₐ: The proportion of women is more than men who exercise regularly, i.e.
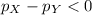`p_(X)-p_(Y)<0`.