Answer:
FC = 28
Explanation:
The parallel lines creates two similar triangles:
ΔBDC similar to ΔEDF
Similar triangle means corresponding lengths are equal.
BD corresponds to ED
BC corresponds to EF
DC corresponds to DF
Now, we want to find FC, we let that length be "x",
thus we can write:
DE similar DF
DB similar DC
So,
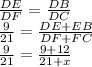
Now, we use algebra, cross multiplication and solve for x, which is FC:
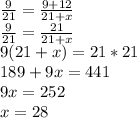
FC = 28