Answer:
= 35.23°
time taken = 0.9898 ns
Step-by-step explanation:
Using Snell's law as:
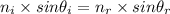
Where,
is the angle of incidence ( 58.0° )
is the angle of refraction ( ? )
is the refractive index of the refraction medium (glass, n=1.47)
is the refractive index of the incidence medium (air, n=1)
Hence,
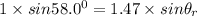
Angle of refraction= sin⁻¹ 0.5769 = 35.23°
The distance it has to travel
d = = 16.5 cm / cos 35.23° = 20.20cm
Also,
n = c/v.
Speed of light in vacuum = 3×10¹⁰ cm/s
Speed in the medium is:
v = c/n = 3×10¹⁰ cm/s / 1.47
= 2.0408 × 10¹⁰ cm/s
The time taken is:
t = d/s
= 20.20 cm / 2.0408×10¹⁰ cm/s
= 9.898 × 10⁻¹⁰ s
= 0.9898 × 10⁻⁹ s
Also,
1 ns = 10⁻⁹ s
So, time taken = 0.9898 ns