Difference between the area of the triangle and square is 25
Explanation:
- Step 1: Find the area of the triangle given its 3 sides using the Heron's formula.
Area of the triangle =
 where s =
where s =
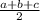
⇒ s = (6 + 8 + 10)/2 = 24/2 = 12
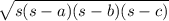 =
=
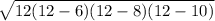
=
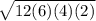 =
=
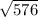 = 24 sq. units
= 24 sq. units
- Step 2: Find the area of the square with perimeter = 28 units.
Perimeter of the square = 4 × side = 28
⇒ Side of the square = 28/4 = 7 units
⇒ Area of the square = (side)² = 7² = 49 sq. units
- Step 3: Find the difference between the area of the square and triangle.
Difference = 49 - 24 = 25