Question

onsider two populations for which μ1 = 38, σ1 = 2, μ2 = 23, and σ2 = 4. Suppose that two independent random samples of sizes n1 = 45 and n2 = 59 are selected. Describe the approximate sampling distribution of x1 − x2 (center, spread, and shape).

Answer 1

Center = 15

Spread = 0.599

Shape = Normal

Explanation:

The provided information is:

`\mu_1=38 \ \ \ \ \ \ \ \ \mu_2 = 23\\\sigma_1 =2 \ \ \ \ \ \ \ \ \ \sigma_2=4\\n_1=45 \ \ \ \ \ \ \ \ n_2 =59`

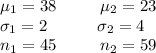
Thus the center(mean) of the distribution is:

`\begin{aligned}Mean &= \mu_1-\mu_2\\&=38-23\\&=15\end{aligned}`

The spread (standard deviation) of the distribution is:

`\begin{aligned}\textrm{Standard deviation}&=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}\\&=\sqrt{(4)/(45)+(16)/(59)}\\&=0.599\end{aligned}`

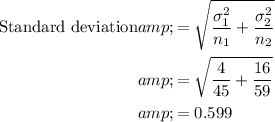
The shape of the distribution is also normally distributed.