Answer:
Center = 15
Spread = 0.599
Shape = Normal
Explanation:
The provided information is:
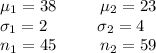
Thus the center(mean) of the distribution is:
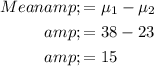
The spread (standard deviation) of the distribution is:
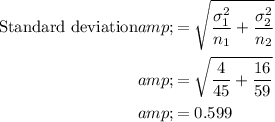
The shape of the distribution is also normally distributed.