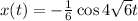Question

A mass weighing 24 pounds, attached to the end of a spring, stretches it 4 inches. Initially, the mass is released from rest from a point 2 inches above the equilibrium position. Find the equation of motion. (Use g

Answer 1

the equation of motion is

`x(t) =-(1)/(6) \cos4√(6) t`

Step-by-step explanation:

Given that,

The weight attached to the spring is 24pounds

Acceleration due to gravity is 32ft/s²

Assume x is the string length, 4inches

convert the length inches to to feet = 4/12 = 1/3feet

From Hookes law , we calculate the spring constant k

k = W / x

k = 24 / (1/3)

k = 24 / 0.33

k = 72lb/ft

If the mass is displace from its equilibrium position by amount x

the differential equation is

`m(d^2x)/(dt^2) + kx=0\\\\(3)/(4 ) (d^2x)/(dt^2)+72x=0\\`

`(d^2x)/(dt^2) +96x=0`

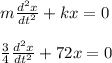
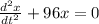
Auxiliary equation is

`m^2+96=0\\m=√(-96) \\m=\_ ^+4√(6)`

Thus the solution is,

`x(t) = c_1cos4√(6t) +c_2sin√(6t)`

`x'(t) =-4√(6c_1) sin4√(6t) +c_24√(6) cos4√(6t)`

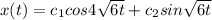
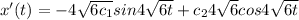
The mass is release from rest

x'(0) = 0

`-4√(6c_1 ) \sin4√(6) (0)+c_24√(6) \cos4√(6) (0)=0\\c_24√(6) =0\\\\c_2=0`

Therefore

x(t) = c₁ cos4 √6t

x(0) = -2inches

c₁ cos4 √6(0) = 2/12feet

c₁= 1/6feet

There fore, the equation of motion is

`x(t) =-(1)/(6) \cos4√(6) t`