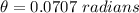Question

A rectangular box has length 20 inches, width 20 inches, and a height of 2 inches. Find the angle between the diagonal of the box and the diagonal of its base. The angle should be measured in radians.

Answer 1

0.0707 radians

Explanation:

Given that:

The dimension of the rectangular box is:

length (l) = 20 inches

width (w) = 20 inches

height (h) = 2 inches

The length of the diagonal of the rectangular box is :

`D_1 = √( l^2+w^2+h^2)`

`D_1 = \sqrt {(20)^2+(20)^2+(2)^2}`

`D_1 = \sqrt {400+400+4}`

`D_1 = \sqrt {804}`

`D_1 = 28.35`

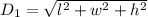
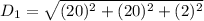
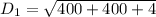
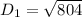
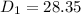
The length of the diagonal of the base of the rectangular box is:

`D_2 = √(l^2+w^2)`

`D_2 = √((20)^2+(20)^2)`

`D_2 = √(400+400)`

`D_2 = √(800)`

`D_2 = 28.28`

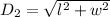
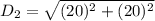
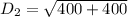
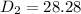
If we take a critical look at a rectangular box; we will realize that the diagonal of the base is the adjacent side & diagonal of the box is the hypotenuse of a triangle formed by the rectangular box.

Therefore, the angle between them is :

`Cos \theta = (Diagonal \ of \ the \ base \ )/(Diagonal \ of \ the \ box )`

`Cos\ \theta = (D_2)/(D_1 )`

`Cos\ \theta = (28.28)/(28.35 )`

`Cos\ \theta = 0.9975`

`\theta = Cos^(-1) \ 0.9975`

`\theta = 4.052^0` to radians

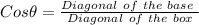
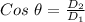
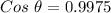
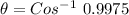
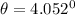`\theta = 0.0707 \ radians`