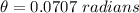Answer:
0.0707 radians
Explanation:
Given that:
The dimension of the rectangular box is:
length (l) = 20 inches
width (w) = 20 inches
height (h) = 2 inches
The length of the diagonal of the rectangular box is :
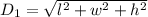
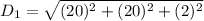
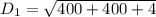
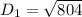
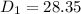
The length of the diagonal of the base of the rectangular box is:
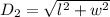
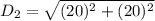
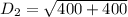
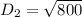
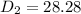
If we take a critical look at a rectangular box; we will realize that the diagonal of the base is the adjacent side & diagonal of the box is the hypotenuse of a triangle formed by the rectangular box.
Therefore, the angle between them is :
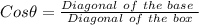
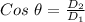
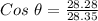
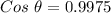
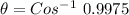
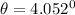 to radians
to radians