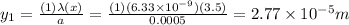Answer:
The first dark fringe is
 away from the central maximum.
away from the central maximum.
Step-by-step explanation:
When you pass a monochromatic light through a small enough slit, light is going to present a diffraction pattern on a screen placed at some distance from the slit. That diffraction pattern consists on dark and bright fringes intercalated. The equation that models this phenomenon is:
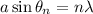
With a the width of the slit, θm the angular position of the nth minimum, n the number of the minimum and λ the wavelength of the incident light. Because the distance of the first minima respect the center of the screen is smaller than the distance of the screen from the slit. we can use the approximation:
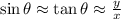
with y the distance of the minimum respect the center of the screen and x the distance of the screen from the slit, then:
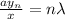
Solving for y1: