Answer:
1.497
Explanation:
If net sales are given by the function:
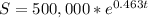
The initial net sales, at t = 0 are:

In order for sales to double, then S(t) must be equal to 1,000,000. The time 't', in years, required for sales to double is:
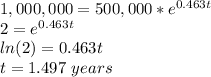
It will take 1.497 years for net sales to double.