Question

A cast-iron flywheel has a rim whose OD is 1 m and whose ID is 0.8 m. The flywheel weight is to be such that an energy fluctuation of 6.75 J will cause the angular speed to vary no more than 200 to 250 rev/min. a) Estimate the coefficient of speed fluctuation. b) If the weight of the spokes is neglected, what should be the width of the rim

Answer 1

A.Coefficient of speed fluctuation of the flywheel = 0.222

B. The width (thickness) of the rim should be 0.131 m (131 mm)

Step-by-step explanation:

A.

Coefficient of speed fluctuation
`(C_(s))`
`= (N_(2)-N_(1))/(N)`

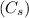
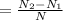
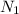`N_(1)` = minimum speed = 200 rpm

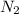`N_(2)` = maximum speed = 250 rpm

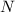`N` = average speed
`= (N_(2)+N_(1))/(2) = (250+200)/(2) = 225 rpm`

∴
`Cs = (250-200)/(225)=0.222`

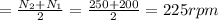
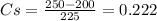
Hence the coefficient of speed fluctuation of the flywheel = 0.222

B.

The moment of Inertia ,
`I=(E_(2)-E_(1))/(C_(s)*\omega^(2))`

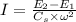
Where

`E_(2)-E_(1)=` energy fluctuation of flywheel = 6.75 J

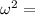`\omega^(2)=` angular velocity of flywheel =
`(2\pi N)/(60) = (2\pi * 225)/(60)= 23.56 rad/sec`

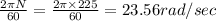
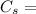`C_(s)=` coefficient of speed fluctuation of the flywheel = 0.222

Hence,

`I=(6.75*10^(3))/(0.222*(23.56)^(2))=54.78 Nms^(2)`

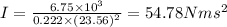
Similarly,

I =
`(m)/(8)*(d_(o)^(2)- d_(i)^(2))`

From the moment of Inertia, we can get the weight of the flywheel as

`m=(8I)/((d_(o)^(2)+ d_(i)^(2)))= (8* 54.78)/((1^(2)+0.8^(2)))=267.22kg`

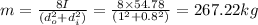
From this weight, we will be able to calculate the volume of the flywheel and hence, estimate the thickness. But to do this, we need to know its density first. this can be got from standard tables.

Specific weight of cast iron =
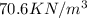`70.6KN/m^(3)` ( from standard material property table)

density of cast iron ,
`\rho =(70.6* 10^(3))/(9.81)= 7,197kg/m^(3)`

Volume of cast iron flywheel =
`(m)/(\rho)= (267.22)/(7197)= 0.03713 m^(3)`

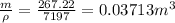
similarly, the volume of the flywheel can also be obtained through the formula :

`V= (\pi t(d_(o)^(2)-d_(i)^(2)))/(4)`

we can easily estimate the thickness of the flywheel from here by solving for t as shown below

`0.03713=(\pi t(1^(2)-0.8^(2)))/(4)`

`0.03713=0.2827t`

`t=(0.03713)/(0.2827)`

`\therefore t= 0.131m \approx 131mm`

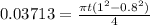
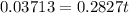
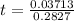
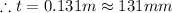
The width of the rim = 131 mm