Question

Find the linear approximation of the function g(x) = 3 1 + x at a = 0. g(x) ≈ Use it to approximate the numbers 3 0.95 and 3 1.1 . (Round your answers to three decimal places.) 3 0.95 ≈ 3 1.1 ≈

Answer 1

`\sqrt[3]{0.95} \approx 0.983\\\\\\\sqrt[3]{1.1} \approx 1.033`

Explanation:

The function is:

`g(x) =\sqrt[3]{1+x}`

We can find a linear aproximation around a point with a Taylor's series:

`g(x)\approx g(a)+g'(a)(x-a)`

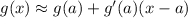
The value of g(a) is

`g(a)=g(0)=\sqrt[3]{1+0}=1`

We have to calculate the firste derivative of g(x):

`g'(x)=(d)/(dx)[(1+x)^ {1/3}]=(1/3)(1+x)^(-2/3)=(1)/(3(1+x)^(2/3))`

Then, we calculate g'(a)

`g'(a)=g'(0)=(1)/(3(1+0)^(2/3))=(1)/(3*1)= (1)/(3)`

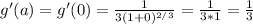
The linear approximation is:

`g(x)\approx1+(1)/(3) (x-0)=(x)/(3)`

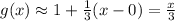
Calculate
`\sqrt[3]{0.95}`

We can use the linear approximation to calculate this, with x=-0.05.

`0.95=1+x\rightarrow x=-0.05\\\\\sqrt[3]{0.95} \approx 1+((-0.05))/(3) =1-0.017=0.983`

Calculate
`\sqrt[3]{1.1}`

We can use the linear approximation to calculate this, with x=0.1.

`1.1=1+x\rightarrow x=0.1\\\\\sqrt[3]{1.1} \approx 1+((0.1))/(3) =1+0.033=1.033`