Complete Question
The diagram for this question is shown on the first uploaded image
Answer:
The differential height is

Step-by-step explanation:
The schematic diagram of the venturimeter is shown on the second uploaded image
The continuity equation is mathematically given as
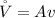
Where A is the area
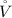 is the flow rate
is the flow rate
 is the velocity
is the velocity
At the inlet making v the subject to obtain the inlet velocity we have
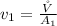
Substituting 124 L/s =
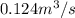 for
for
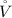 and
and
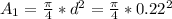 given that
given that
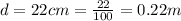
So
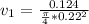

At the exit point the velocity is
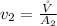
Where
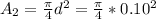 given that
given that
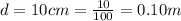
So
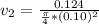
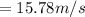
The Bernoulli's flow equation between the inlet and exist is mathematically given as
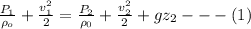
And
![P_1 - P_2 = \rho_o [(v_2^2)/(2) + (v_1^2)/(2) ] = \rho_(water) gh ---(2)](https://img.qammunity.org/2021/formulas/physics/college/p6iqb3eubx1dtdfwg2tzzqfh47xcimegiu.png)
Where
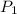 is the pressure at inlet
is the pressure at inlet
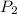 is the pressure at exist
is the pressure at exist
 is the density of water with value of
is the density of water with value of
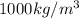
g is acceleration due to gravity
h is the height of the water column
making h the subject in the equation 2
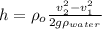
where
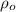 is the density of air given in the question
is the density of air given in the question
Substituting value

