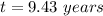Question

If $5200 is invested at a rate of 8.6% compounded quarterly, how long will it take, to the nearest hundredth of a year, until the investment is worth $11,600

Answer 1

`t= 9.43\ years`

Explanation:

we know that

The compound interest formula is equal to

`A=P(1+(r)/(n))^(nt)`

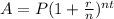
where

A is the Final Investment Value

P is the Principal amount of money to be invested

r is the rate of interest in decimal

t is Number of Time Periods

n is the number of times interest is compounded per year

in this problem we have

`t=?\ years\\ P=\$5,200\\ r=8.6\%=8.6\100=0.086\\n=4\\A=\$11,600`

substitute in the formula above

`11,600=5,200(1+(0.086)/(4))^(4t)`

`11,600=5,200(1.0215)^(4t)`

`(11,600/5,200)=(1.0215)^(4t)`

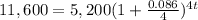
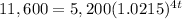
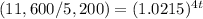
Applying log both sides

`log(11,600/5,200)=log(1.0215)^(4t)`

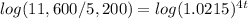
applying property of logarithms

`log(11,600/5,200)=(4t)log(1.0215)`

`t=log(11,600/5,200)/[(4)log(1.0215)]`

`t= 9.43\ years`