Question

A guitar string is strummed near a tuning fork that has a frequency of 512 Hz. Initially, the guitar and tuning fork together create a sound wave with a beat frequency of 5 Hz. The tension in the guitar string is then increased, after which the guitar and tuning fork together create a sound wave with a beat frequency of 4 Hz. After the tension in the guitar string is increased, is the frequency of the guitar string:

Answer 1

The question is incomplete. However, I have made an attempt to guess what the question is asking for.

Answer:

The original frequency of the guitar string is 507 Hz.

The frequency is increased after the tension is increased.

Its new frequency is 508 Hz.

Step-by-step explanation:

The tuning fork has a frequency of 512 Hz.

With a beat frequency of 5 Hz, the guitar has a frequency of

• 512 - 5 = 507 Hz OR
• 512 + 5 = 517 Hz

The relationship between frequency, f, and tension, T, is given by

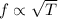`f\propto√(T)` provided other factors are constant.

It follows that when tension is increased, frequency increases.

Therefore, when the tension in the string is increased, its frequency increases.

From the question, this increase in frequency caused a reduced beat frequency of 4 Hz.

This means the new frequency is

• 512 - 4 = 508 Hz OR
• 512 + 4 = 516 Hz

In the first choice, there is an increase in the frequency from 507 Hz to 508 Hz.

The second choice indicates a decrease from 517 Hz to 516 Hz.

Since we have established there is an increase in frequency, the first choice is correct. The original frequency of the guitar string is 507 Hz.